List Combinations Of N Items Taken M At A Time
July 02, 2021 - by Bill Jelen

Challenge: You want to list all unique combinations of m items from a population set of n items. For example, you might want to generate all possible unique groups of 4 employees from a set of 10.
Solution: There are two ways to go about this: the quick-and-dirty way and the better-but-more-difficult way.
Quick-and-Dirty Solution
An unimaginative (and rather kludgey) approach to solving the problem for m=3 could be:

A major problem with this approach is that the number of For ... Next loops is hard-coded in the routine. If you need to find combinations of, say, 4 items at a time, an additional For ... Next loop has to be inserted, and the condition check needs to be modified. For combinations of 2, a loop would need to be removed or skipped.
A Better Solution
This problem is an ideal candidate for a recursive function. This solution comprises a subroutine to specify the inputs n (population set size) and m (subset size), initialize a combinations counter, and set things up for entry of the combinations in column A of the active worksheet. This routine then calls a recursive function to generate the combinations. After all combinations are generated, the program exits, with a message with information on the number of combinations found.
Copy the following code to a blank module in a workbook:
Dim NumComb ‘Combinations counter
Sub Combinations()


The Sub procedure is fairly straightforward. The power play begins from the point where the function is called:
Comb2 n, m, 1, ""Let’s start by analyzing how to logically build the combinations. Let’s say you want to generate combinations of 5 items taken 3 at a time (i.e., output 3 characters from 1,2,3,4,5). You would build the strings as follows:
- Starting with 1, add values sequentially until your subset has a size of 3. The next value is 2, so you get 1,2. The following value is 3, so you get 1,2,3, at which point your subset size of 3 elements is attained. Then you look for other combinations by varying the third value, and you get 1,2,4 and 1,2,5. Thus with 1,2 you get 1,2,3 and 1,2,4 and 1,2,5.
- Increment the second value to 3 to get the two-piece fragment 1,3. The third value in sequence is 4, so you get 1,3,4, at which point your subset size of 3 elements is attained. Then you look for other combinations by varying the third value, and you get 1,3,5. Thus with 1,3 you get 1,3,4 and 1,3,5.
- Increment the second value to 4 to get the two-piece fragment 1,4. The third value in sequence is 5, so you get 1,4,5, at which point your subset size of 3 elements is attained. In your quest for other combinations by varying the third value, you find none because 5 is already used. Thus with 1,4 you get 1,4,5 only.
- Increment the second value to 5 to get 1,5. You find that you have no next value for the third element.
- Increment the first value to 2, set the second element to 3, and get the combinations 2,3,4 and 2,3,5 and so on to get the remaining combinations 2,4,5 and 3,4,5.
Let’s now examine the function Comb2. Notice the ByVals in the function arguments, which cause arguments to be passed by value. When first called from the subroutine (Comb2 n, m, 1, “”), for our example of 5 items taken 3 at a time, the arguments are n=5, m=3, k=1, and a null string indicating that the 3-element string is yet to be built.
At the initial entry point, the two Ifs (which we look at more closely later) are skipped. The line executed is:
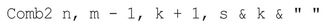
Notice that this is a call to the function itself (which is why it is called a recursive function), with m reduced by 1 (m=2 now) , k incremented by 1 (k=2 now), and the string being set to “1 “. The code again skips the two Ifs, and the line Comb2 n, m - 1, k + 1, s & k & " " calls the function recursively again, with m=1, k=3, and s="1 2 " and then with m=0, k=4, and s="1 2 3 ". At this point, you have obtained the first combination.
When the same line calls the function next, the condition m=0 is satisfied, and the code enters this block:

This part of the code enters the combination (‘1 23‘) in the active cell, activates the next cell, and exits the last call to the function. Remember that the function was last called by:
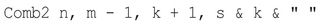
The Exit function makes it branch to the next line, Comb2 n, m, k + 1, s. At this point, the last value in the string (“1 2 3”) is incremented to the extent possible to get “1 2 4” and “1 2 5” in subsequent calls. When “1 2 5” is obtained, the next call by Comb2 n, m, k + 1, s is done with m=1 and k=6.
These values of m and k satisfy the condition for If m > n - k + 1 Then Exit Function because 1 > 5 – 6 + 1 and the call to the function exits, signifying the end of the loop for combinations for 12*.
The function thus continues to run, building the combinations for 13*, 14*, 23*, 24*, and 34*, and it finally exits to the Sub Combinations function from which it was first called, and a message box says that 10 combinations were generated.
An easy way to monitor the flow of calculations is to uncomment the line Debug. Print m, k, s in the code for Comb2 and watch the output in the immediate window:
| m | k | s |
|---|---|---|
| 3 | 1 | |
| 2 | 2 | 1 |
| 1 | 3 | 1 2 |
| 0 | 4 | 1 2 3 |
| 1 | 4 | 1 2 |
| 0 | 5 | 1 2 4 |
| 1 | 5 | 1 2 |
| 0 | 6 | 1 2 5 |
| 1 | 6 | 1 2 |
| 2 | 3 | 1 |
| 1 | 4 | 1 3 |
| 0 | 5 | 1 3 4 |
| 1 | 5 | 1 3 |
| 0 | 6 | 1 3 5 |
| 1 | 6 | 1 3 |
| 2 | 4 | 1 |
| 1 | 5 | 1 4 |
| 0 | 6 | 1 4 5 |
| 1 | 6 | 1 4 |
| 2 | 5 | 1 |
| 3 | 2 | |
| 2 | 3 | 2 |
| 1 | 4 | 2 3 |
| 0 | 5 | 2 3 4 |
| 1 | 5 | 2 3 |
| 0 | 6 | 2 3 5 |
| 1 | 6 | 2 3 |
| 2 | 4 | 2 |
| 1 | 5 | 2 4 |
| 0 | 6 | 2 4 5 |
| 1 | 6 | 2 4 |
| 2 | 5 | 2 |
| 3 | 3 | |
| 2 | 4 | 3 |
| 1 | 5 | 3 4 |
| 0 | 6 | 3 4 5 |
| 1 | 6 | 3 4 |
| 2 | 5 | 3 |
| 3 | 4 |
Summary: This topic illustrates how a problem that would otherwise require a variable number of For...Next loops can be efficiently solved using a subroutine/recursive function combination.
Source: Tracking all combinations on the MrExcel Message Board.
Title Photo: Ellen Qin on Unsplash
This article is an excerpt from Excel Gurus Gone Wild.
