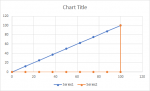
Sure. When presenting a plot, it should be easy for the reader to understand what the author is attempting to convey. In this case, there are two curves plotted in x-y space, but there are no clear indicators showing how the curves relate to each other or what they mean. It appears that you selected the % people column and the % income earned column and constructed an x-y (scatter) chart, but it is not clear what was used for the x data...because if you selected just two arrays of data, and then made an x-y scatter chart, you would get only one plotted set of points (or one curve) showing x vs. y. You have two curves. It appears that you may have added a second plot, essentially plotting the % people points against themselves to create the Equality Curve, but this is a point of confusion.
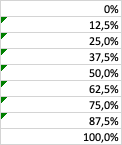
When constructing a Lorenz Curve, the plot limits are (1,1), meaning 100 % on the x-axis for percentile of people and 100 % on the y-axis of cumulative income. That would typically be constructed with just two points: (0,0) and (1,1), and those data points are typically hidden...you want only the line connecting the two. Yet you show a number of data points along the equality line, which leads one to wonder where the x-data are to support that line.
Axis labels help to explain the relationships depicted by the data. My original point was that in order to produce a true step in the Lorenz Curve, you would have to add an extra data point to force a 90 degree vertex at location (100,0). But based on my understanding of Lorenz Curves, I do not believe that is advisable. Generally, arbitrarily adding a data point to a data set is a bad idea because you would be representing that the added data point means something about the phenomena being presented. In this case it would not: 100 % of the people cannot simultaneously be responsible for 0 % and 100 % of the earned income.
Instead, the data are indicating that 87.5% of the people represented make no money; and the remaining 12.5% of the people account for all of the earned income. This represents a gross disparity in income equality, and the large area between the Equality Curve and the Lorenz Curve illustrate this. As for the plot title, the plot does not really show the Gini Coefficient, but rather it shows the Lorzenz Curve. One can determine the Gini Coefficent from the data. The worksheet where I played around with the data and plots is available at the link below (I would normally post a sample of the worksheet using XL2BB, but that doesn't support embedded plots as far as I know). I suspect you want to show two sets of data: one to create the Equality Curve, the other to create the Lorenz Curve...see Data Set C in the file for an example. which was used to produce the plot shown here. I've also added the triangular area calculations that are used to determine areas for the Gini Coefficient calculation.

www.dropbox.com