Best ZScore scaling

[JenniferMurphy]

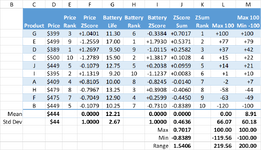
I am working on a macro to generate a composite rating for products that are rated on multiple properties. I convert each separate rating to a z score. This puts them all on a common scale. (Mean = 0, Standard Deviation = 1.) I then add up the z scores.

With z scores, it is a little difficult to get a good sense of the relative ratings. The table below has ratings for price and battery life. The corresponding z scores are in columns D & G. The sum of the z scores is in column I. Product D gets the top rating of 2.2812. In second place is Product I with a z score of 2.2556. But how much better is D than I.

My first thought was to "scale" the z scores so that the top score = 100 and the rest retain their relative value in proportion to that one. That is the contents of column K. That looks a lot better to me. We are used to rating things as percentages, so the 100 max looks good. Now we can see that D is less than 2 points better than I, but there is then is a gap of over 25 points to Product A in 3rd place.

I like that the z scores have a mean of zero. That says to me that the ones with a negative sore are less than average.

But I noticed that the lowest score is not -100. In some cases, it can be a lot lower. So my next thought was to scale it so that the top is 100 and the bottom is -200. That result is in column L.

I would appreciate any comments or suggestions. Thanks

Weighted Ratings.xlsx
	B	C	D	E	F	G	H	I	J	K	L	M
5		Product	Price	Price ZScore	Price Rank	Battery Life	Battery ZScore	Battery Rank	ZScore Sum	ZSum Rank	Max 100	Max 100 Min -100
6		D	$389	+1.2697	1	9.50	+1.0115	2	+2.2812	1	+100.00	+100.00
7		I	$395	+1.1319	2	9.20	+1.1237	1	+2.2556	2	+98.88	+99.04
8		A	$409	+0.8105	4	10.00	+0.8245	3	+1.6350	3	+71.67	+75.75
9		G	$399	+1.0401	3	11.30	+0.3384	5	+1.3785	4	+60.43	+66.13
10		B	$449	-0.1079	5	10.25	+0.7310	4	+0.6231	5	+27.32	+37.78
11		J	$449	-0.1079	5	12.75	-0.2038	6	-0.3117	6	-13.66	+2.71
12		F	$475	-0.7049	7	12.90	-0.2599	7	-0.9648	7	-42.29	-21.80
13		H	$479	-0.7967	8	13.25	-0.3908	8	-1.1875	8	-52.06	-30.15
14		C	$500	-1.2789	10	15.90	-1.3817	9	-2.6606	9	-116.63	-85.43
15		E	$499	-1.2559	9	17.00	-1.7930	10	-3.0489	10	-133.66	-100.00
16	Mean		$444	0.0000		12.21	0.0000		0.0000		0.00	14.40
17	Std Dev		$44	1.0000		2.67	1.0000		1.9455		85.29	73.00
18	Max							Max	2.2812
19	Min							Min	-3.0489
20	Range							Range	5.3301
Scaling

Cell Formulas
Range	Formula
E6:E15	E6	=-([@Price]-TblScalings[[#Totals],[Price]])/PriceStdDev
F6:F15	F6	=RANK.EQ([@[Price ZScore]],[Price ZScore])
H6:H15	H6	=-([@[Battery Life]]-TblScalings[[#Totals],[Battery Life]])/BattStdDev
I6:I15	I6	=RANK.EQ([@[Battery ZScore]],[Battery ZScore])
L6:L15	L6	=[@[ZScore Sum]]/ZSumMax*100
M6:M15	M6	=(([@[ZScore Sum]]-ZSumMin)/(ZSumRange)*200)-100
L16	L16	=SUBTOTAL(101,[Max 100])
M16	M16	=SUBTOTAL(101,[Max 100 Min -100])
L17	L17	=STDEV.S(TblScalings[Max 100])
M17	M17	=STDEV.S(TblScalings[Max 100 Min -100])
K6:K15	K6	=RANK.EQ([@[ZScore Sum]],[ZScore Sum])
D16	D16	=SUBTOTAL(101,[Price])
E16	E16	=SUBTOTAL(101,[Price ZScore])
D17	D17	=STDEV.S(TblScalings[Price])
E17	E17	=STDEV.S(TblScalings[Price ZScore])
G16	G16	=SUBTOTAL(101,[Battery Life])
H16	H16	=SUBTOTAL(101,[Battery ZScore])
G17	G17	=STDEV.S(TblScalings[Battery Life])
H17	H17	=STDEV.S(TblScalings[Battery ZScore])
J6:J15	J6	=[@[Price ZScore]]+[@[Battery ZScore]]
J16	J16	=SUBTOTAL(101,[ZScore Sum])
J17	J17	=STDEV.S(TblScalings[ZScore Sum])
J18	J18	=MAX(TblScalings[ZScore Sum])
J19	J19	=MIN(TblScalings[ZScore Sum])
J20	J20	=J18-J19

Named Ranges
Name	Refers To	Cells
BattStdDev	=Scaling!$G$17	H6:H15
PriceStdDev	=Scaling!$D$17	E6:E15
ZSumMax	=Scaling!$J$18	J20, L6:L15
ZSumMin	=Scaling!$J$19	J20, M6:M15
ZSumRange	=Scaling!$J$20	M6:M15

 

[sijpie]

I would think it to be better if you don't have negative scores, but go from 100 to 10 (no product has zilch value), or if you really want, 100 to 0.

 

[JenniferMurphy]

I would think it to be better if you don't have negative scores, but go from 100 to 10 (no product has zilch value), or if you really want, 100 to 0.

Thanks. I came to the same conclusion, more or less.

I started with 10 products with fictional data about price and battery life. How would you rate them if you wanted to minimum price and maximize battery life? A better battery life tends to correlate with a higher price. Note that the prices are ranked in ascending order, whereas the battery life values are ranked in descending order.

We can sort them by price or by battery life, but not both.

It’s difficult to compare these two sets of data. Not only are they two completely different scales, but they are in the opposite order. The best prices are the lowest, whereas the best battery life values are the highest. Sorting one tends to reverse sort the other. This is where z-scores can be useful. Let’s convert both the prices and battery life data to z-scores. Note that, as with the ranks above, we used the standard formula for the battery life z-scores, but reverse (negative) formula for the prices. Adding them should give us a sense of the combined ratings. That sum is in Column J. It tells us that Product G has the best combination of price and battery life. It ranked #3 on price and #6 on battery life. Product E is second and Product D is third.

Z-scores make it possible to combine multiple ratings and see how the products rank overall. It’s easy to see which one is best and next best, but not easy to tell by how much. In this case, they are all fractional numbers less than 1. It’s a little difficult to get a good sense of the relative strengths.

My first thought was to scale the z-scores so that the top score is 100. That way the scores would be more like percentages, with which most people are more familiar. To do that, divide the scores by the maximum z-score then multiply by 100.

The results are in Column L. These values seem easier to understand than the ones in Column J. Product G is 23 points ahead of E.

The “-120” for Product B bothered me a bit. I didn’t like the asymmetry. I decided to scale the z-scores from +100 to -100. The formula for that is:

These results are in Column M. The symmetry has been achieved and the scores are tighter overall due to being spread across a shorter range. Now Product E is just 21 points behind G.

I thought mapping the scores onto a range of +100 to -100 would allow the reader to pay attention to the positive scores and reject the negative ones. But then I realized that if my goal is to simulate percentages, the negative scores don’t really fit. My next try was to scale the scores to a range of 100 to 0. The formula for that is a bit simpler than the previous one.

These results are in Column N. Of the four options (J, L, M, & N), I think N is the cleanest and clearest. The scores are tighter and more like actual percentages. And it eliminates the plus and minus signs.

Note: The numbers are not actual percentages. Product G does not meet 100% of the user’s requirements nor does B meet none (0%) of them. G meets 100% of the product that best meets the user’s requirements. The definition of B’s 0% rating is less clear.